Checking if gsl_integration_qng() will work

At the end of part 1, I suggested that gsl_integration_qng() would not be able to successfully integrate the function we want to find the Fourier series of. Here is the function I will find the Fourier series of.

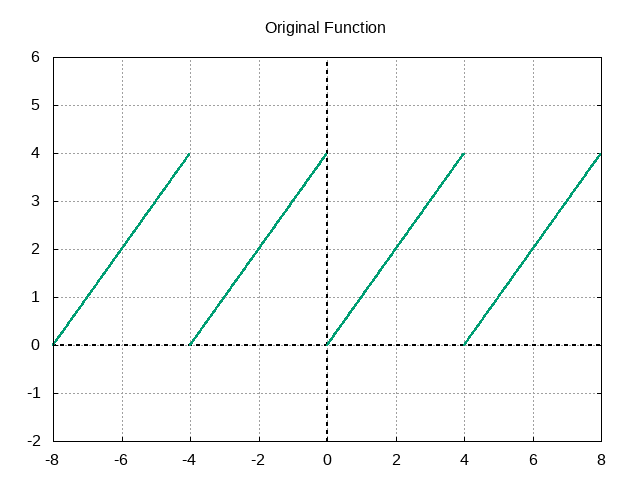
Because this function is discontinuous, we have to approximate it with a Fourier series instead of a Taylor series. If we recall the formulas shown in the last part, we know that we will have to integrate $f(x)$ from $0$ to $2l$, among other things. Before calculating the Fourier series, let's try using gsl_integration_qng() to perform basic integration.

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_integration.h>

/* f(x) = x for 0 <= x < 4, repeating */
double f(double x, void *params) {
  const double period = 4;
  return fmod(x, period);
}

int main() {
  double result, error;
  double low = 0, high = 8;
  gsl_function F = {.function = &f};
  double err_abs = 0, err_rel = 1;
  size_t num_evals;

  gsl_integration_qng(&F, low, high,
      		err_abs, err_rel,
      		&result, &error, &num_evals);
  printf("result error num_evals\n");
  printf("%f %f %zu\n", result, error, num_evals);
}

Results:
|    result |    error | num_evals |
| 14.804436 | 8.015135 |        21 |

Well, something happened here, but it's not quite what we wanted. We told GSL to take gsl_integral-i. Since we're dealing with a discontinuous function, we can rewrite this as gsl-integral-rewrite-i. Now I'm no mathematician, but this answer should be 16, not 14.8. Additionally, our error is very large, and if I attempt to lower err_rel to a smaller value, GSL yells at me saying that it failed to reach the requested error.

This is not a problem on GSL's end. We aren't using the right integration function for the job! According to the GSL manual,

The QNG algorithm is a non-adaptive procedure which uses fixed Gauss-Kronrod-Patterson abscissae to sample the integrand at a maximum of 87 points. It is provided for fast integration of smooth functions.

While that's a lot of words, the important part is the last sentence. gsl_integration_qng() is for smooth functions. Our function is not smooth, it has a discontinuity! We will need to find an alternative function in GSL that can handle discontinuous graphs.

gsl_integration_qng() and discontinuities

Fortunately we do not have to look far. The very next function mentioned in the manual is what we need. gsl_integration_qag() has the following signature.

int gsl_integration_qag(const gsl_function * f,
            double a, double b,
            double epsabs, double epsrel,
            size_t limit, int key,
            gsl_integration_workspace * workspace,
            double * result, double * abserr)

f, a, b, epsabs, epsrel, result, and abserr are all the same as gsl_integration_qng(). We can see that several new terms are introduced however.

workspace is a pointer to an area of memory used by gsl_integration_qag. We allocate space by using the gsl_integration_workspace_alloc() function, This function is passed an integer to adjust how much memory we want to allocate. Whatever integer we pass to gsl_integration_workspace_alloc()we need to ensure that limit is the same. This way, gsl_integration_qag knows how much memory it has available.

key is a integer between 0 through 6. GSL recommends using higher values when integrating smooth functions, and lower values when functions are discontinuous.

Let's see how well gsl_integration_qag() performs!

#include <stdio.h>
#include <math.h>
#include <gsl/gsl_integration.h>

double f(double x, void *params) {
  const double period = 4;
  return fmod(x, period);
}

int main() {
  size_t limit = 1024;
  gsl_integration_workspace *w
    = gsl_integration_workspace_alloc(limit);
  double result, error;
  double low = 0, high = 8;
  gsl_function F = {.function = &f};
  double err_abs = 0, err_rel = 1e-7;

  gsl_integration_qag(&F, low, high,
      		err_abs, err_rel,
      		limit, 1, w,
      		&result, &error);
  /* get into the habit of freeing memory when done! */
  gsl_integration_workspace_free(w);
  printf("result error\n");
  printf("%f %f\n", result, error);
}

Results:
| result | error |
|   16.0 |   0.0 |

Look at that! We are getting the exact value we expected, even though we're integrating with a discontinuity. We are now at the point where we can calculate the Fourier series for our function.

Generating our Fourier series

Let's recall that we can find our $a_n$ and $b_n$ coefficients with the following formulas.

GSL expects us to only pass one function to it as an argument. That means that, unlike before, we can't just pass a pointer to our function f(x), as GSL won't be multiplying it by the cosine and sine terms.

There are a couple of solutions to this that I can think of. The first is to make use of the void * argument that GSL includes in the gsl_function structure. Using this, we could pass extra information to f(x), adapting it to our specific n value.

Alternatively, we could write a parent function, like aorb_subn(). This function would then be stored in the gsl_function structure. The advantage of this approach is that the function we want the Fourier series of, f(x), is distinct in our code. This should make it a bit easier to change f(x) to any function that we want. This is the approach that I will take.

To make this code hopefully a bit more modular, I moved the integration out of main, and instead into a function called get_aorb_subn(). This function calculates the nth Fourier coefficient for a function f(x), using the variable get_a to determine if it should calculate $a_n$ or $b_n$. It may be better to wrap this in a fourier structure that contains the two terms, but I elected not to do that to hopefully maintain some vague semblance of readability.

This is what the code to calculate the Fourier series looks like.

#include <stdbool.h>
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_integration.h>

#define PI 3.14159
const double period = 4;
const double l = period / 2;

struct aorb_params {
  double (*f)(double x, void *params);
  int n;
  bool calc_a;
};

double f(double x, void *params) {
  return fmod(x, period);
}

double aorb_subn(double x, struct aorb_params *params) {
  int n = params->n;
  double trig = params->calc_a ? cos(PI*n*x/l) : sin(PI*n*x/l);
  return params->f(x, NULL) * trig;
}

double get_aorb_subn(double (*f)(double x, void *params), int n,
      	       double low, double high, bool get_a) {
  double normalization = 1/l;
  if (get_a && n == 0) normalization /= 2;

  size_t limit = 1024;
  gsl_integration_workspace *w
    = gsl_integration_workspace_alloc(limit);
  double result, error;
  gsl_function F = { .function = &aorb_subn,
    .params = &(struct aorb_params){ .f = f, .n = n,
      		 .calc_a = get_a } };
  double err_abs = 0, err_rel = 1e-7;

  gsl_integration_qag(&F, low, high,
      		err_abs, err_rel,
      		limit, 1, w,
      		&result, &error);
  gsl_integration_workspace_free(w);

  return normalization * result;
}

int main() {
  const int upto = 10;
  double a_subn[upto], b_subn[upto];
  double low = 0, high = period;

  for (int i = 0; i < upto; i++) {
    a_subn[i] = get_aorb_subn(f, i, low, high, true);
    b_subn[i] = get_aorb_subn(f, i, low, high, false);
    printf("%d %f %f\n", i, a_subn[i], b_subn[i]);
  }
}

Results:
| n | a_subn |    b_subn |
|---+--------+-----------|
| 0 |    2.0 |       0.0 |
| 1 | -7e-06 | -1.273242 |
| 2 | -7e-06 | -0.636621 |
| 3 | -7e-06 | -0.424414 |
| 4 | -7e-06 |  -0.31831 |
| 5 | -7e-06 | -0.254648 |
| 6 | -7e-06 | -0.212207 |
| 7 | -7e-06 | -0.181892 |
| 8 | -7e-06 | -0.159155 |
| 9 | -7e-06 | -0.141471 |

Like I mentioned before, aorb_subn is a "parent function" that combines f(x) and the sine/cosine term. This is the function we integrate, and we provide it enough information to know what term we are calculating.

Interestingly, if we use the $\pi$ constant M_PI, the integration fails due to roundoff error. Fortunately we can get "close enough" values by just using a few less digits.

Once we graph the Fourier series generated by these coefficients, this is what we get.

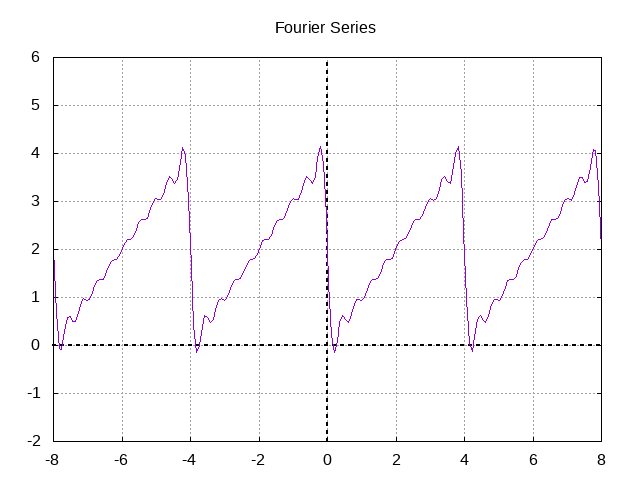
And there we are! Here is a Fourier series generated for a discontinuous periodic function. The more terms we add, the more accurate the approximation.